Perhaps to no one’s surprise, I’m writing yet another article on content that I’m studying for my qualifying exam. Apparently, I figure that I can point to this when I inevitably fail my exam, but I digress. Let’s talk about the Lisp programming language and how to design an interpreter for it.
Table of Contents
- Lisp Overview
- Lisp S-Expressions
- Lisp Syntax
- Lisp Semantics
- Lisp Interpreter Design
- Want to Learn More?
Lisp Overview
Honestly, I hadn’t touched any functional programming until I started playing around with languages like Haskell and Scheme in my Sample Programs in repo. Of course, eventually I learned about Lisp as a part of a programming languages course at The Ohio State University. Naturally, I have an exam on this very subject in just over a week, so let’s dig in.
First off, Lisp is one of the oldest programming languages—second to FORTRAN, I believe. Of course, Lisp differs from FORTRAN quite a bit in that it’s a functional programming language. In other words, there’s no notion of state or side-effects. Instead, computations are expressed through functions and expressions rather than statements.
In this article, we’ll talk about a fairly limited form of Lisp which only has a handful of builtin functions. As a result, don’t expect to be able to pass any of the code we discuss directly into a Scheme interpreter or anything like that.
Lisp S-Expressions
In order to grasp Lisp, it’s important to understand its design. Specifically, everything in Lisp is a symbolic expression or s-expression which is a text-based way of expressing a binary tree. In other words, instead of drawing out a binary tree, we can write one using parentheses and dots:
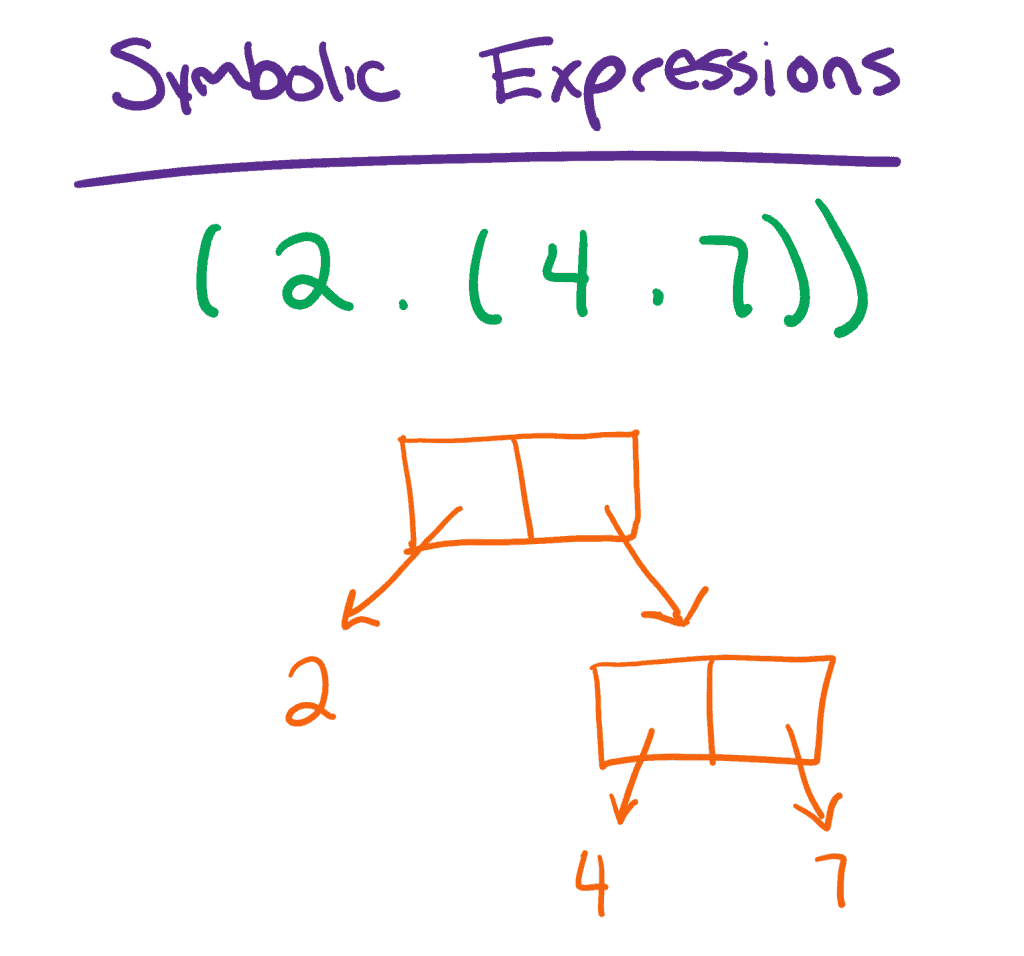
Of course, the smallest possible s-expression is called an atom. As the name implies, an atom is an indivisible programming element like a number or a function name. In this case, atoms are what get stored in the leaves of the binary tree.
In Lisp, these s-expressions are all we need to understand to be able to grasp the language. After all, everything else is built on top of them.
Lisp Syntax
Given what we know about s-expressions, let’s take a look at a simple Lisp grammar as provided in the slides for the CSE 6431 course at OSU:
<atom> ::= <numeric atom>
| <literal atom>
<numeric atom> ::= <numeral>
| -<numeral>
| +<numeral>
<numeral> ::= <digit>
| <numeral><digit>
<literal atom> ::= <letter>
| <literal atom><letter>
| <literal atom><digit>
<letter> ::= a
| A
| b
| B
| …
| z
| Z
<digit> ::= 0
| 1
| 2
| …
| 9
<S-exp> ::= atom
| (<S-exp> . <S-exp>)
In its simple form, Lisp is composed of s-expressions which can either be standalone atoms or nested s-expressions of the form (<s-exp> . <s-exp>).
From there, we define two productions for atoms. On one hand, they can be integers of arbitrary size or literals which are essentially strings.
All that said, most forms of Lisp include yet another s-expression production called the list:
list ::= (<items>)
| ()
items ::= <S-exp>
| <S-exp> <items>
In other words, a list would look like a space-separated collection of s-expressions. Of course, as a binary tree, a list looks as follows:
Lisp Semantics
At this point, we’ve looked quite a bit at what Lisp looks like, but we haven’t talked a lot about how Lisp actually works. For example, the following code snippet is perfectly valid Lisp syntax, but what does it do?
(cons (cdr ′(11 . 6)) (car ′(4 . 5)))
In this case, we’ll generate a new s-expression that looks like (6 . 4), but how would we know that? As it turns out, Lisp has a ton of builtin functionality.
CONS
First, we should talk about how we can build up our binary trees using a function called cons. cons, short for construct, creates an s-expression from two s-expressions:
(cons 4 7)
In this example, cons is supplied two atoms: 4 and 7. As a result, cons returns an s-expression of the form (4 . 7).
Naturally, we can nest cons calls to create more interesting s-expressions:
(cons (cons 1 2) 3)
In this case, the inner cons would construct (1 . 2) which would then be combined with 3 to form ((1 . 2) . 3).
CAR and CDR
First, we should talk about the two s-expression traversal functions: car and cdr. I call them traversal functions because they allow us to access nodes in our binary trees. For example, if we had the s-expression (3 . 7), we could return the left s-expression, 3, using car and the right s-expression, 7, using cdr.
Interestingly enough, car and cdr are often extend to provide even deeper nesting functionality. For example, cadr would grab the right s-expression using cdr then grab the left s-expression of the child using car.
In situations where we have atoms, car and cdr and their extended forms have undefined behavior. In other words, they should return an error.
ATOM, INT, and NULL
In addition to the traversal functions, there are a handful of unary functions which can be used to test s-expressions for various properties.
One of those unary functions is called atom, and like the other two unary functions, it accepts one s-expression as input (i.e. (atom 5)) If the s-expression is an atom, the function returns T. Otherwise, it returns NIL.
Naturally, both int and null perform similarly. In particular, int returns T if the s-expression is an integer and NIL otherwise. Likewise, null returns T if the s-expression is NIL and NIL otherwise.
As you can probably imagine, these three functions are useful when writing custom functions. For example, if we want to write a function which can find the smallest element in a list, a null check would be a good place to start.
PLUS, MINUS, TIMES, QUOTIENT, and REMAINDER
Like most programming languages, there has to be some way to perform arithmetic. Of course, in a purely functional language, operators are replaced by functions. For instance, addition might look as follows:
(plus 2 7)
In total, there are five arithmetic functions in Lisp—plus, minus, times, quotient, and remainder—and they correspond to addition, subtraction, multiplication, division, and remainder, respectively.
LESS, GREATER, and EQ
In addition to the arithmetic functions, there are also relational functions similar to less than, greater than, and equals in other languages. For example, the check if two values are equal, we would use the EQ function:
(eq 7 2)
In this case, the expression evaluates to false because 7 is not equal to 2. Naturally, all three of these functions work similarly.
QUOTE
One of the interesting features of Lisp is how everything gets evaluated in the interpreter. Each time the interpreter encounters an expression, it attempts to evaluate it. As a result, there are expressions which seem valid to us but are not to the interpreter. For example, the following might seem fine:
(atom (2 3 5))
Unfortunately, this will crash because (2 3 5) has to be evaluated. Naturally, it has no semantic meaning, so the interpreter tries to treat it like a function. Since 2 isn’t a function name, the interpreter crashes with an error:
2 is not a function name; try using a symbol instead
Instead, we can use the quote function to say to the interpreter: “return this value without evaluating it.”
(atom (quote (2 3 5))
As you can imagine, quote can really blow up a code base, so most versions of Lisp have some form of syntactic sugar as follows:
(atom '(2 3 5))
Now, that’s slick! And of course, this expression now returns NIL.
COND
Another interesting feature of Lisp is the ability to build up control flow similar to a switch statement:
(cond
(b1 e1)
(b2 e2)
...
(bn en)
)
Here, each boolean expression is evaluated from b1 to bn until one of the expressions returns T. The passing expression then executes its corresponding expression. For example, if b2 evaluates to T then e2 is evaluated.
Naturally, we can use this syntax for more interesting logic which we’ll get to in the next section.
DEFUN
Finally, there’s a syntax for creating our own functions called defun. In general, the syntax is as follows:
(defun f (x y) z)
Here, the function name is denoted by f, and the function parameters are denoted by the list containing x and y. Ultimately, the function body is denoted by z.
Based on all the functions we’ve covered up to this point, Lisp functions must be recursive, right? After all, there are no loops in Lisp, so any sort of repetition must be accomplished exclusively through function calls. For example, if we wanted to write a function to search a list for a value, it might look as follows:
(defun find (val list)
(cond
((null list) nil )
(T (cond
((eq val (car list)) T )
(T (find val (cdr list)))))))
Honestly, I don’t know what the best indentation would be here, but this function gets the job done. It works by first checking if the input list is null. If it is, then we’re done. Otherwise, we check to see if the first value in the list is what we want. If it is, we return true. Otherwise, we run a recursive call on the remainder of the list.
If we want to use our new find function, we call it as follows:
(find 4 `(3 7 2 4))
Since 4 is in this list, we return T as expected.
At this point, we’ve covered just about everything about the syntax and semantics of Lisp. Now, let’s get into the interpreter design.
Lisp Interpreter Design
As it turns out, we can actually use Lisp to define our Lisp interpreter—aka bootstrapping. In particular, we’ll be looking at the interpeter from the point of view of the top-level eval function.
EVAL
As the name states on the tin, eval evaluates a Lisp s-expression. However, in addition to the s-expression, a eval function requires a bit of context in the form of two lists: the association list (a-list) and the function definition list (d-list).
Specifically, the a-list stores all parameter bindings within the current scope in the following form:
((parameter1 . binding1) (parameter2 . binding2) ...)
Meanwhile, the d-list stores all function definitions in the following form:
((function_name1 (param_list1 . body1)) (function_name2 (param_list2 . body2) ...)
Unlike like the a-list, the d-list is global and consequently one of the few parts of Lisp that introduces side-effects.
At any rate, these two lists are then passed to eval which has the following body:
eval(exp, a_list, d_list) =
[atom[exp] ->
[eq[exp, T] -> T |
eq[exp, NIL] -> NIL |
int[exp] -> exp |
bound[exp, a_list] -> getval[exp, a_list] |
T -> ERROR!]
T ->
[eq[car[exp], quote] -> cadr[exp] |
eq[car[exp], cond] -> evcon[cdr[exp], a_list, d_list] |
eq[car[exp], defun] -> add to d_list |
T -> apply[car[exp], evlist[cdr[exp], a_list, d_list], a_list, d_list]]]
Now, that’s surprisingly simply. In fact, this alone is the interpreter. Obviously, there are a few undefined functions here and even some pseudocode, but this is incredibly elegant.
In the first of eval, we deal with atoms only. In particular, we handle the three main atoms—T, NIL, and integers—as well as any symbol bindings such as variables. If we find a symbol binding with bound, we return that binding using getval.
In the second half of eval, we deal with everything else. First, we check if the left element of our s-expression is quote, cond, or defun, and then we apply whatever makes sense for those three special functions. Otherwise, we attempt to apply whatever symbol we see.
In the next few sections, we break down some of these undefined functions.
EVCON
Whenever we have a set of conditions, we use a special function called evcon to evaluate them:
evcon[cond_list, a_list, d_list] =
[null[cond_list] -> ERROR! |
eval[caar[cond_list], a_list, d_list] -> eval[cadar[cond_list], a_list, d_list] |
T -> evcon[cdr[cond_list], a_list, d_list]
As expected, evaluating a set of conditions is pretty simply. If there are no conditions, we throw an error. If the current condition evaluates to T, we evaluate its expression. Otherwise, we grab the next condition, and recursively call evcon on it.
EVLIST
Like evcon, evlist is also a pretty simple helper function. It’s main role is to evaluate each expression in a list, and return a new list with all of the expressions evaluated:
evlist[arg_list, a, d] =
[null[arg_list] -> NIL |
T -> cons[eval[car[arg_list], a_list, d_list], evlist[cdr[arg_list], a_list, d_list]]]
With evlist, we iterate over the list while evaluating each expression. Each result is then combined with the result of a recursive call on the remainder of the list. The result should be a list of evaluated s-expressions.
APPLY
Finally, we bring the interpreter home with an implementation of the apply function:
apply[fname, arg_list, a_list, d_list] =
[atom[fname] ->
[eq[fname, car] -> caar[list] |
eq[fname, cdr] -> cdar[list] |
eq[fname, cons] -> cons[car[list], cadr[list]] |
eq[fname, atom] -> atom[car[list]] |
eq[fname, eq] -> eq[car[list], cadr[list]] |
int, null, plus, minus, less, etc. |
T -> eval[cdr[getval[fname, d_list]],
addpairs[car[getval[fname, d_list]], list, a_list],
d_list]
] |
T -> ERROR! ]
Naturally, apply is a bit bigger than all the other functions because we have to perform manual checks for each of our builtin functions: car, cons, plus, null, etc.
Of course, the most interesting part of the apply function is the last case which covers user-defined functions. In that case, we bind the formal parameters to the function arguments using addpairs and place the results in the a-list. Then, we evaluate the function body with the new bindings in the a-list.
And, that’s it! That’s the entire Lisp interpreter written in mathematical notation for Lisp. Overall, the interpreter looks like its about 30 or 40 lines of code, but my buggy Java implementation is much larger .
.
Want to Learn More?
Naturally, there’s a lot more I can cover in terms of Lisp, but I think that’s enough for today. After all, I have a lot more studying to do.
If you liked this article and you’d love to get content like this sent directly to your inbox, subscribe to The Renegade Coder newsletter. As always, you’re welcome support the site directly through Patreon as many people already do. Your support goes a long way to keeping educational content like this free to the public.
as many people already do. Your support goes a long way to keeping educational content like this free to the public.
If you’re looking to pick up any Computer Science books, might I suggest a few:
- Common Lisp Recipes: A Problem-Solution Approach
 by Edmund Weitz
by Edmund Weitz - Land of Lisp: Learn to Program in Lisp, One Game at a Time!
 by Conrad Barski
by Conrad Barski
As always, I try to find good resources for my readers, but you’re welcome share some of your own. Alternatively, you can always stick around. Here are few functional programming articles:
At any rate, thanks again for your support. If this is your first time reading my work, let me know what you think of it in the comments!
Recent Posts
It's July 2024, and I have three chapters of my dissertation drafted! Two more and we'll be ready to defend.
In growing the Python concept map, I thought I'd take today to cover the concept of special methods as their called in the documentation. However, you may have heard them called magic methods or even...

