In the process of building out my “Autodidact’s Guide to Python” series, I was writing an article about algorithmic thinking. In that article, I said the following:
On a side note: it might be fun to create a series of articles this way. Define a high-level guide to doing a mundane task then go way down the rabbit hole writing how-to guides for every little detail.
I thought this would be fun because we sometimes forget how much work actually goes into performing simple tasks—which is why it’s often difficult to get a computer to replicate reality. To prove that to you, I figured we could define some mundane task and try to continually peel back layers of abstraction until we have almost no idea what we’re talking about. And, if nothing else, I’m excited to take this opportunity to learn something new. With that said, let’s get started.
Table of Contents
- Defining the Mundane Task
- Choosing an Approach
- Anticipating Challenges
- Setting the Groundwork for the Series
Defining the Mundane Task
I am a bit nervous about this part of the article because the task we choose could leave us with an incredible amount of work to do. As a result, we need to pick something that is simple enough to be conveyed in a few abstract steps while complex enough to be broken down into more detailed pieces.
Ultimately, what I’m imagining is some task which we could explain to the average person in a couple of sentences, and they would know exactly what to do. However, if we were giving that same set of steps to an alien (or computer), we would need to give significantly more details.
Because I love internet memes, I figured we could work with something simple like opening a jar:
In the words of SpongeBob, “easy!”, right?
Choosing an Approach
The way I think about defining algorithms is through levels of abstraction. In other words, each algorithm can be represented as a hierarchy or tree. At the root of this tree, we have the problem where trying solve. Then, the first layer of the tree is the highest level of abstraction.
If our algorithm is a tree, then there are a lot of different ways we can traverse this tree. In general, there are two main ways to do this: depth-first and breadth-first.
Through depth-first traversal, we might start by defining the first step, which according to SpongeBob is to “get a jar.” Then, instead of defining the second step, we actually break down this first step into substeps. This approach is a bit problematic in our case because we could potentially generate substeps for eternity. For example, the first step to getting a jar might be to look for a jar. Meanwhile, the first step of looking for a jar might be to scan the room. From there, we might define the first step of scanning the room as opening our eyes. Do you see an end in sight?
On the flip side, a more appropriate approach for us might be to follow a breadth-first traversal. To do that, we would define all of the steps at the highest abstraction first. According to SpongeBob, that would be (1) to “get a jar” and (2) to “take the lid off the jar.” Because Patrick fails when given these directions, we have to go down a level of abstraction to provide more explicit directions. This will be the approach we take in this series.
Unfortunately, the downside to this breadth-first approach is that each level of abstraction is exponentially larger than the previous level. As a result, over the course of this series, we’ll be tackling one branch at a time. For example, this article will outline the first two steps according to SpongeBob. In the next article, we’ll break down the first step into a set of substeps. By the end of the third article, we will have completed the second layer of the algorithm. If there’s enough interest, we’ll try to define the third layer while working through each branch one at a time.
Anticipating Challenges
Now that we’ve defined the problem and we have a structure for how we’re going to go about it, we need to talk about some of the challenges ahead. The only challenge that comes to mind for me is control flow.
Right now, the tree concept is very easy to grasp because the steps are sequential without any jumps. What I anticipate happening is complexity being introduced when we begin breaking down certain steps. For example, I might break down the “get a jar” task into three subtasks:
- Look for a jar
- Approach the jar
- Pick up the jar
Again, because of how abstract these tasks are, we can proceed from step to step without issues. However, we start to run into issues when we break down the steps any further. For instance, how would you specify approaching the jar? To me, that seems like an iterative task where the individual repeatedly makes certain movements until some goal is reached.
This becomes a problem for our tree structure because the branches at any given level are intended to be the set of steps to complete the task. If we introduce control flow, we suddenly have to find ways to represent that on the tree—or do we?
I think we can still treat all the children of a node as the set of instructions for that particular task. However, we won’t show the relationship between those children. In other words, if one task is repeated in a loop, we don’t need to explicitly show that in the tree. The only thing that will need to be shown in the tree is the condition that we need to check.
Outside of the control flow issue, I don’t anticipate anything else coming up, so let’s go ahead and define the first level of abstraction for our tree.
Setting the Groundwork for the Series
If you watched the SpongeBob video above, then you know that the correct way to open a jar can be conveyed in two steps:
- Get a jar
- Take the lid off of the jar
As a tree, this algorithm looks as follows:
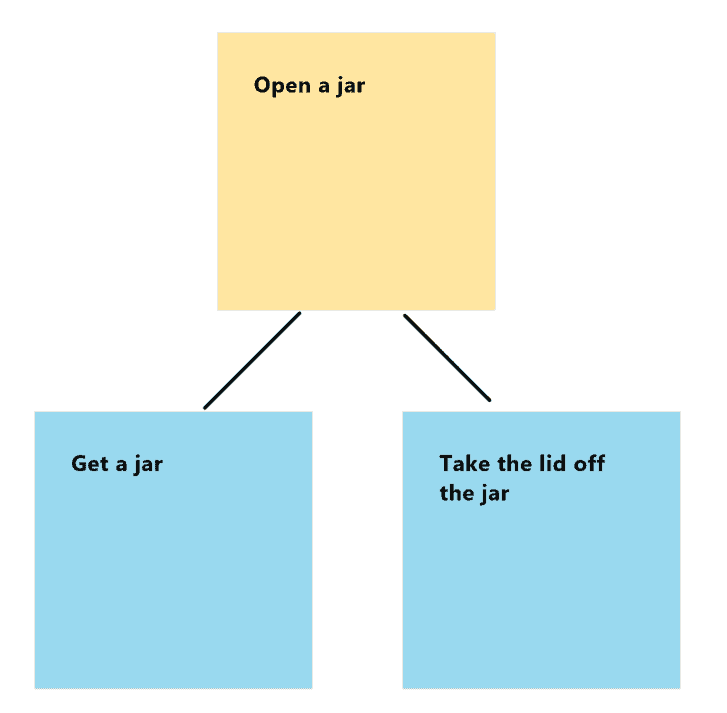
In the next article, we’ll break down the steps for getting a jar. After that, we’ll talk about what goes into taking the lid off the jar. For now, this will all seem pretty straightforward, but I’m actually pretty excited to start talking about silly things like “how to open your eyes” and “how to walk toward an object.” I’m hoping these sort of things allow me to merge some of my interests like physics and programming.
Depending on how long this series goes, it might be interesting to take whatever algorithm we end up with at the end and try to implement it in code. I don’t anticipate writing an algorithm that will actually open a jar, but it might be interesting to try to implement some functions that could be used to open a jar.
With that said, we’ll call it right here! If you’re excited about this series and would like to know when the next article is coming out, feel free to head over to my list of ways to grow the site. There you’ll find my newsletter as well as links to other things like Patreon, Discord, and Twitter. Otherwise, take care and see you next time!
Recent Blog Posts
It's July 2024, and I have three chapters of my dissertation drafted! Two more and we'll be ready to defend.
Meritocracy: The Facade That Determines Who Deserves Success
On a drive home from a bachelor party, I was so bored that I got to thinking about meritocracy and its consequences. It's amazing what the mind can do.

