Welcome back to yet another tutorial on data structures. In this 4th installment of the series, we’ll take a look at our first complex data structure – the stack. Don’t worry! It’s not actually complicated. It just builds on our knowledge of linked lists. So if you’re not familiar with linked lists, now is probably a good time to revisit them.
Table of Contents
What is a Stack?
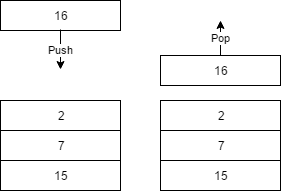
If we think back to our lesson on methods, we’ll remember that Java stores method calls on the stack. But what exactly is a stack? Like its name implies, a stack is a data structure which resembles a stack of items. We can think about it like a pile of papers or a stack of pancakes. That’s because a stack only allows us to add or remove items from the top. As a result, stacks really only support two operations: pop and push.
As we can probably imagine, the push operation involves placing a new item on top of the stack. Meanwhile, the pop operation performs the opposite. These two functionalities alone are all we need to create a stack. However some stacks have additional features like peek which allows us to check the top node without having to pop it off the top.
Properties of Stacks
Stacks are basically just special case linked lists (though they can be implemented using arrays). In other words, we keep the same structure of a linked list, but we only expose pop and push. As a result, we can’t traverse a stack. Instead, we interact with the data structure exclusively through the top element.
Restricting a linked list gives us some pretty interesting new properties. For one, a stack is a last-in first-out (LIFO) data structure. This structure allows us to keep track of the state of a system in a recursive manner. For example, Java uses braces to define code blocks. However, sometimes we nest several levels before we close a block. If we want to track these braces, we might intuitively think that we can just count the number of open and close braces. If the numbers match, we’re good. Unfortunately, that sort of method would fail. After all, starting a program with a close brace is a compilation error.
Instead, we can track the braces using a stack. Every time we encounter an open brace, we pop it on top. If we encounter a close brace, we peek at the top for any open braces. If one exists, we pop it off and continue. Otherwise, we know we have a compilation error! 🙂
Applications of Stacks
Due to the recursive nature of the stack, we have quite a few fun applications for them. The classic example is reversing a string. We would simply push each letter onto the stuck and then pop them back out. That reversing behavior actually comes in handy if we ever want to reverse the state of a system. Think undo. In fact, the universal undo command (ctrl + z) is likely implemented using a stack.
We can actually use a stack to implement backtracking as well. Think about maze traversal. In a maze, we start by storing each move on a stack. Eventually, we’ll run out of moves. If the maze is not solved by that point, we would then backtrack until we hit a location where we had some unused moves. This process would continue until we solved the maze.
Of course, compilers make heavy use of stacks for matching braces. This is especially applicable for languages like Java and C/C++ which use braces to signify code blocks.
Java Stack Syntax
Like linked lists, Java also has support for the Stack data structure. Stacks come in two primary forms: static and dynamic. We can really think about these two implementations as arrays vs. linked lists. For the purposes of this tutorial, our stack will be implemented as a linked list (aka dynamic). For more information on static stacks, feel free to check out this implementation of an ArrayStack
in Java.
Class Definition
Because a stack is really a linked list in disguise, the class definition is going to look quite similar.
public class Stack {
private Node top;
}
And that’s pretty much it. Notice that we actually hide the top node. We only want to expose push and pop for the purposes of encapsulating the underlying linked list structure.
The Node class we’re using is the same node from the last lesson. It’s only going to work with integers as generic types are still a bit out of scope. However, we’ll get around to those soon enough!
Insertion
As stated before, there’s really only one way to perform an insertion on a stack. It’s called a push. A push is clearly a constant time operation. We simply insert a node at the front of the list and reset the head.
public void push(int value) {
this.top = new Node(value, this.top);
}
With this method, we can push values on top of the stack forever. When we want to start clearing it, we’ll need an implementation of pop.
Deletion
Since stacks are so simple, it makes sense to show off at least one more piece of syntax: deletion. Like insertion, deletion is a fixed cost operation which we call pop.
public int pop() {
if (this.top != null) {
Node toRemove = this.top;
this.top = this.top.getNext();
return toRemove.getPayload();
} else {
throw new NoSuchElementException();
}
}
In the case that the stack is empty, we throw an exception. Otherwise, we remove the node and return the element to the user.
Summary
That’s about all we have for stacks. As always, here’s the breakdown of the typical data structure operations and their Big O estimates. Like linked lists, stacks perform great with insertion and deletion. However, they don’t really support access and search. It’s possible to implement both of those features, but then we’d essentially have a linked list.
| Algorithm | Running Time |
|---|---|
| Access | O(N) |
| Insert | O(1) |
| Delete | O(1) |
| Search | O(N) |
Thanks for sticking around for another tutorial on data structures. Up next we’ll cover the queue!
Recent Posts
As the semester starts to wrap up, I'm a bit busy and a bit burnt out. As a result, I thought I'd have a little fun writing about nasty little bugs I've run into over time. I'll keep it short; don't...
I find the structure of relational databases to be appealing. They allow you to store data in various tables that eliminate redundancy, reduce storage size, and combine easily. Therefore, it should...