Welcome back to another Java tutorial! If you are following along, then you just finished playing around with numbers in DrJava’s interactions pane. In this tutorial, we will be giving some context to some of the examples from the previous tutorial. In particular, we’ll be covering Java primitive types and their role in variable creation. Let’s get started!
Table of Contents
Concepts
Before we really dig into the code, we need to talk about primitive types and their capabilities.
Java Primitive Types

In every programming language, there are data types that are built-in to the language. In languages like Java where all data types are explicit, each one has a unique keyword. These explicit keywords are used to tell the language what type we want to use when we create variables:
variableType variableName; // Declaration variableName = variableValue; // Definition
The syntax above is how we create and store data in a variable. We start by declaring the type of the data we want to store followed by its name. This portion of the syntax is called the variable declaration. Then, we define the variable using the assignment operator (=) and some value. Of course, it’s much easier to create variables in a single line:
variableType variableName = variableValue;
In Java, we can define a variable using one of the eight built-in data types which we call primitive types: int, double, char, byte, short, long, float, and boolean. For example, we might define an integer as follows:
int height = 17;
In this case, we’ve defined a variable called height with a value of 17. Naturally, we’ll need to become familiar with all eight primitive types, so we can use them appropriately.
Java Relational Operators
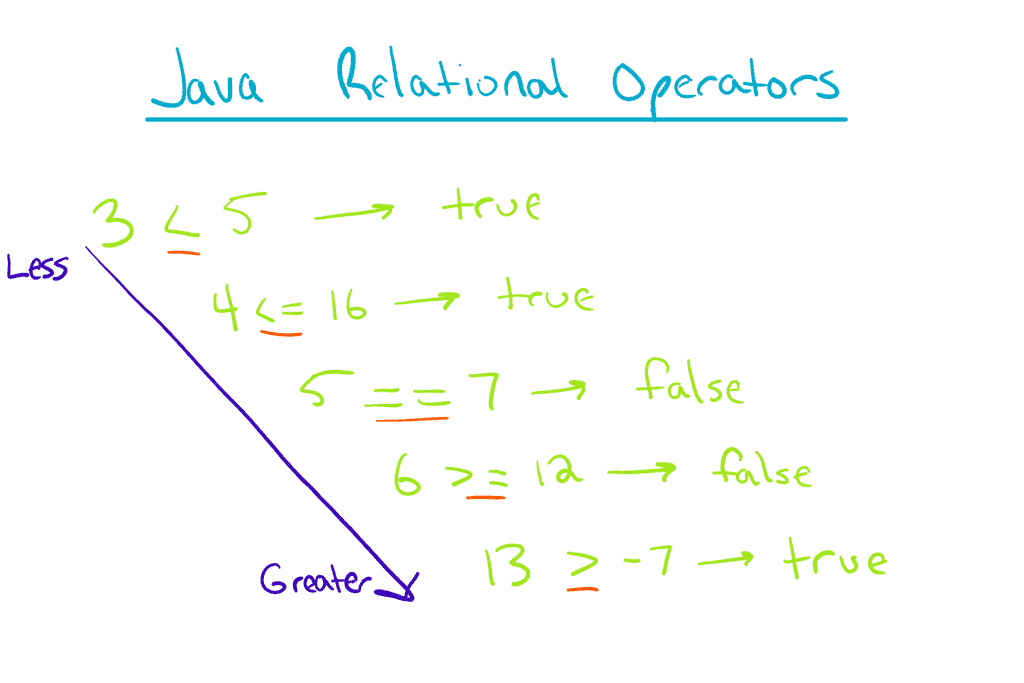
Just above, we talked about storing a numeric value in a variable. That said, Java can do a lot more than store numbers. For example, we can compare numbers using the relational operators.
In the previous tutorial, we were exposed to one of these operators: ==. In addition, we can compare values using !=, <, <=, >, and >=. Try some of the following examples:
6 > 7 // 6 is greater than 7 (false) 110 >= 54 // 110 is greater than or equal to 54 (true) 95 < 96 // 95 is less than 96 (true) 63 <= 100 // 63 is less than or equal to 100 (true)
As you have probably noticed, the result of each of these operations is a boolean value: true or false. In the future, we will see these operators being used to drive all sorts of logic.
Java Arithmetic Operators

While the relational operators are fun, we need arithmetic operators to make our expressions more interesting. Up to this point, we have introduced arithmetic operators at random without really explaining them. Fortunately, we’ll take a look at all of the most common Java arithmetic operators: +, -, *, /, %.
To start, try running the following expressions and pay attention to the comments:
2 + 3 // 2 plus 3 (5) 11 - 5 // 11 minus 5 (6) 13 * 2 // 13 times 2 (26) 6 / 3 // 6 divided by 3 (2) 11 % 2 // remainder of 11 divided by 2 (1)
In this case, we’ve executed all five operators on integers. It’s a good idea to get familiar with what would happen if you ran each operator on the various primitive types. For example, try using the double type:
2.0 + 3.0 // 2.0 plus 3.0 (5.0) 11.0 - 5.0 // 11.0 minus 5.0 (6.0) 13.0 * 2.0 // 13.0 times 2.0 (26.0) 6.0 / 3.0 // 6.0 divided by 3.0 (2.0) 11.0 % 2.0 // ERROR! Can't compute remainder on doubles
As we’ll see in the next section, things get weird when we mix the types in our expressions.
Truncation
While arithmetic might seem straightforward, there are some pitfalls we should be aware of. After all, what do we expect to happen when we start to mix primitive types? For example, the following expressions return different results:
1 + 2 // 3 1 + 2.0 // 3.0
It might seem silly, but this distinction can have consequences. For instance, what happens if we swap addition for division? As it turns out, something like 1 / 2 will result in a value of 0. In computer science, we call this truncation.
Truncation occurs because 32-bit integers can only hold discrete values. Instead of rounding the output, integers just drop any bits that do not fit in the 32-bit window. This is true for all of the data types, but it is often easier to notice with integers.
While truncation can be confusing and counter-intuitive, it comes in handy in some instances such as mapping—we will definitely be exposed to this later.
At any rate, as long as our types are consistent, arithmetic is pretty simple. However, if we are forced to mix compatible types such as integer and double, Java converts the entire result to the widest type. In other words, the type that has the most bits will be the result of the computation.
Numeric Limits
Another potential issue with arithmetic is wraparound. As it turns out, numbers in computer systems have limits, and computations can sometimes exceed those limits.
If you had a chance to read up on the 8 primitive types, then you’ll know that there’s a quick way to check the limits of each primitive type. As a refresher, we can determine the maximum value of an integer using the following code snippet:
Integer.MAX_VALUE
The return value might seem confusing at first, but we will quickly realize that the value is half of the possible range. That must mean the other half of the range is composed of negative values. Try using the following as confirmation:
Integer.MIN_VALUE
For fun, let’s see what happens when we push beyond these limits:
Integer.MAX_VALUE + 1 // Prints -2147483648 Integer.MIN_VALUE - 1 // Prints 2147483647
Isn’t that odd? We’ve just observed integer wraparound for the first time. In other words, once we’ve hit the limit of a primitive type, we’ll wraparound to the other side. Keep that in mind as we move forward.
In case it wasn’t already clear, a data type which has its range split between negative and positive values is called a signed type. Likewise, a data type which has an entirely positive range is called an unsigned typed. In either case, the language interprets the bits representing a value.
Type Casting
Perhaps the last topic to touch on for primitive types is this notion of type casting. We already talked about type widening where a computation gets stored in the widest type. Type casting is just the opposite.
Let’s say we had a computation that would result in a double, but we did not care about the decimal result. We can cut the precision using a typecast to integer. This is used all over the place in code, but a good example would be an implementation of rounding. Without any knowledge of control flow, we can implement rounding:
int round = (int) (7.6 + 0.5);
In this example, the number we are trying to round to the nearest whole number is 7.6. If the decimal is less than .5, we want the result to round down. Likewise, if the decimal is .5 or greater, we want the result to round-up.
By adding .5, we force 7.6 to become 8.1. The typecast then truncates the decimal point which results in our properly rounded integer. If the number was 7.4, the computation would force 7.4 to 7.9. Then the typecast would truncate the decimal.
With that in mind, we have covered just about everything we might need to know about the Java primitive types.
Practice
At this point, we should be quite familiar with a handful of concepts including:
- Variable declarations and definitions
- 8 primitive types:
boolean,int,double,float,byte,short,long,char - 5 arithmetic operators:
+,-,*,/,% - 5 relational operators:
==,>=,>,<,<= - Truncation
- Type casting
- Numeric limits
At this point, we’ll bring it all together with some examples. In the interactions pane, try the following:
char letter = 'b';
Earlier, we wrote a similar line where we assigned a variable a value of 7. In that case we were working with integers. In this case, we are working with the char primitive type which can store character values. With this line, we have now stored our own value in a variable called letter. Go ahead and experiment with the various data types. For instance, we might try any of the following:
boolean hasMoney = true; int hour = 7; double height = 13.7; float gravity = 9.81f; long sixBillion = 6000000000L;
Now that we have some variables declared, try adding some of these values together and note the results. For instance:
hour + height;
The variable names do not make a lot of sense, but this is perfectly legal and will result in 20.7. However, if we try something like:
hasMoney + hour;
We will end up with an error. That is because we’re trying to add a boolean to an integer. Meanwhile, the following is completely legal in Java:
char gravity = 'g'; char speedOfLight = 'c'; gravity + speedOfLight;
We can indeed add these characters together which yields 202 or ‘Ê’. Because the char type is actually a numeric value, we can sum them like integers.
Adding characters is particularly handy if we want to compare characters for ordering. For instance, two letters can be compared alphabetically by comparing their numeric values. A complete list of all the available ASCII characters and there values can be found here .
.
As an added note, Java characters are 16-bit which gives them much greater variety than the 256 ASCII characters. In addition, the char primitive type is the only Java primitive type that is unsigned.
But What About Strings?
Since we’re on the topic of characters, let’s talk strings. Java has native support for strings which are sequences of characters. However, strings are not a Java primitive type. They are instead a reference type.
A reference type is a bit different from a primitive type. With primitive types, we are free to copy and compare data as needed. This makes development extremely intuitive because of this concept called value semantics. Value semantics imply that variables are immutable, so we don’t have to worry about a copy corrupting the original value.
To test this concept, try the following in DrJava’s interactions pane:
int x = 5; int y = 5; y == x;
Notice that this comparison returns true as expected. Intuitively, 5 equals 5. Now try the following:
String firstName = "Leroy"; String lastName = "Leroy"; firstName == lastName;
In this example, we define two components of someone’s name: Leroy Leroy. Intuitively, we would think comparing both names would return true. After all, both names have the same letters and both names are case-sensitive. However, we get a shocking result of false.
As it turns out, the == operator does not compare the strings as expected. The reason for the bad comparison will be explained in more detail in the following tutorial, so for now try comparing more strings. For instance, we could try creating two strings and assigning them to each other:
String firstName = "Leroy"; String lastName = "Jenkins"; firstName = lastName; firstName == lastName;
In this case, the comparison using == results in true. Of course, the value comparison is the same, so why would it return true this time? In the next tutorial, we will take a deeper look at strings and what is really happening when we make a comparison using ==.
Be careful! If you use almost any tool other than DrJava’s interactions pane, you may find that expressions like "Leroy" == "Leroy" return true. This is due to a special feature of Java called string interning (thanks, Iven
(thanks, Iven ) which ensures that duplicate string constants have the same reference. In other words, we still aren’t comparing the contents of the string. More on that later!
) which ensures that duplicate string constants have the same reference. In other words, we still aren’t comparing the contents of the string. More on that later!
Recent Posts
It's July 2024, and I have three chapters of my dissertation drafted! Two more and we'll be ready to defend.
In growing the Python concept map, I thought I'd take today to cover the concept of special methods as their called in the documentation. However, you may have heard them called magic methods or even...

