Welcome to the first article in a ten-part series on the introduction to coding in Java. If this is your first time coding, you’ve come to the right place. Let’s get started!
Table of Contents
Java Background
Java is a programming language that popped on the scene in 1995 from a company called Sun Microsystems now known as Oracle Corporation. In terms of capabilities, Java is a high level programming language which is both object-oriented and strongly typed—we’ll get to both of these concepts later.
If Java had a claim to fame, it would probably be its portability. All code is compiled to byte code and executed on the Java Virtual Machine or JVM. This allows a developer to write code on almost any platform and transfer it between platforms.
But, let’s back up! You’re probably here because you want to know the very basics of Java. Rather than getting bogged down with a lot of theory, you probably prefer to get your hands on some examples. In these tutorials, I’ll start every section by visiting some of the concepts that I feel you will need to know.
With the theory out of the way, we’ll tackle a couple examples. If this series isn’t enough for you, here are some additional resources:
Of course, we can’t get to any of that if we never get started, so let’s get to work.
The Basics of Logic
Before we can get into programming, we need to get an idea of how a computer works at a low level. To do so, we’ll need to cover the following concepts: computer processors and logic gates.
Computer Processors
At the center of every computer is a processor which handles all of the thinking for the system. However, processors don’t think in the way that you or I do. They work by taking commands and computing their results.
At a high level, commands come in the form of mathematical computations, but it’s actually more interesting than that. When we issue a command to the processor, it actually changes how electricity flows through its circuits.
We can think of the processor as a series of wires and switches which direct the flow of current through a circuit. At each junction, a switch can be flipped open which allows current to pass from the input of the junction to the output. Likewise, a switch can block the flow of current when flipped closed.
In logic, we use a special kind of switch called a transistor. For the sake of scope, we won’t get into how they work, but you’re welcome to explore the subject a bit more before finishing up here.
Logic Gates
Now to make these transistors useful, we usually combine them to form a logic gate. A logic gate is a configuration of transistors characterized by a truth table. In other words, we can describe a logic gate by how it responds to all possible inputs. We then summarize our findings in a truth table.

For simplicity, we typically refer to an input as ON or 1 when there is current on it. Otherwise, we refer to that input as OFF or 0.
We can then use this knowledge to give some meaning to a few of the basic logic gates: AND, OR, NAND, and NOR. These gates control the flow of electricity in a circuit by only producing current on the output under special conditions. For instance, an AND gate only opens if all of its inputs have current on them. In other words, all of the inputs are ON or 1.
The opposite of the AND gate is the NAND gate which only produces current on the output if none of the inputs have current on them. In other words, all the inputs must be OFF or 0. In the next section, we’ll take a look at what this means for developers.
An Introduction to Binary
With some basic logic under our belt, we can now go up one level of abstraction. In particular, we’ll cover number systems and bits.
Number Systems
The zeroes and ones that are used to describe interactions with logic gates are the same units a computer uses in programming. These units are described using a number system called binary. Binary is a base 2 number system where the two possible values are 0 and 1.

In contrast, humans have decided to use a base 10 number system (possible values are 0-9). The beauty of binary is that we can start representing numbers based on the flow of electrons in a circuit. Unfortunately, the logic gates above only have a single output. Imagine what we could do if we had more outputs.
As an example, let’s say we have a circuit that has four outputs. If each output can have a value of zero or one, how many possible output combinations can there be?
Well, each output can have one of two values, so we multiply the number of combinations for each output (2 x 2 x 2 x 2). In total, we can have 16 combinations which can give us a decimal range of 0-15. So regardless of what this circuit does, we can start recording results as decimal numbers.
Bits and Bytes
In the example above, our circuit had four binary outputs which tells us the bit count of the circuit. In other words, our circuit was 4-bit.
If we know how many bits a system has, computing the total range of values is actually pretty easy: raise two to the number of bits. For example, a 16-bit system would have a total range of values of 216 or 65,536 possible values.
If dealing with binary wasn’t confusing enough, we can actually put bits into groups of eight which we refer to as bytes. In other words, a 16-bit system may also be referred to as a 2-byte system. From there, 1,024 bytes is a kilobyte, 1,024 kilobytes is a megabyte, and so on.
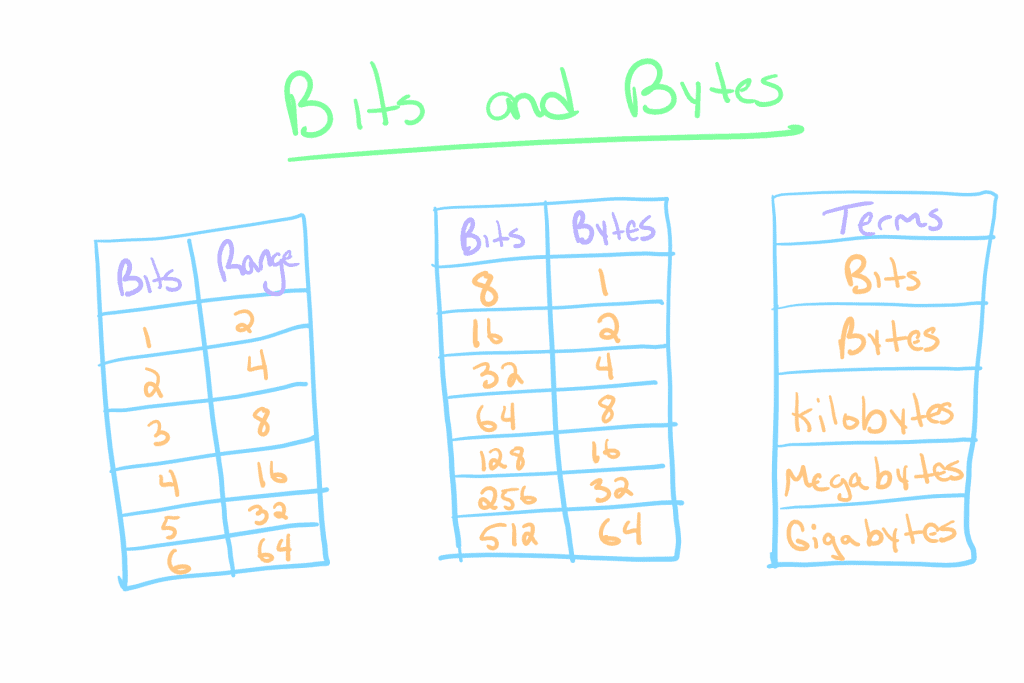
Keep these concepts in the back of your mind when we you start playing around with Java numbers.
Introduction to Coding in Java
Perhaps the best way to start learning is to begin tinkering with numbers in Java. Unfortunately, the majority of Java tools don’t provide facilities for this because Java is compiled, not interpreted. In other words, Java has a specific layout that needs to be followed before we can begin testing. This can be quite cumbersome to new learners, so we plan to go over each piece in steps.
For now, I recommend downloading DrJava because it provides a convenient workaround. This workaround is called the interactions pane and it lets us start playing with code snippets.
Once DrJava is downloaded, let’s use the interactions pane to start doing basic math. The following are some examples of combinations that we could try:
is downloaded, let’s use the interactions pane to start doing basic math. The following are some examples of combinations that we could try:
5 + 7 5 + 7.0 3 - 4 3 - 4.0 1 / 2 1 / 2.0 6 * 6 6 * 6.0 4 % 5 4 % 5.0
If you liked these examples, I recommend checking out the Java Number Exploration Lab. While the article is targeted at fellow teachers, you may find that the content is well suited for beginners like yourself.
Congratulations! We just finished our first Java tutorial. Stay tuned and we’ll chat about what exactly is happening with the results.
Recent Posts
It's July 2024, and I have three chapters of my dissertation drafted! Two more and we'll be ready to defend.
In growing the Python concept map, I thought I'd take today to cover the concept of special methods as their called in the documentation. However, you may have heard them called magic methods or even...


