It’s midsemester, and I’ve been buried in my dissertation proposal. That said, I wanted to take a minute to help some of my students out who are working through recursion right now. Here are 5 tips for making sense of the topic.
Table of Contents
- Just Don’t
- Consider the Classes of Recursive Problems
- Build Confidence; Don’t Trace
- Draw a Picture
- Pivot to a Language Where Recursion Is the Norm
Just Don’t
It might sound funny, but one of my first tips for making sense of recursion is to ignore how it actually works at first. If you’re going to use recursion as a tool, you need to be able to write code that makes use of it. To do that, it’s often a lot easier to memorize a process for generating recursive solutions.
If you’re wondering what that process looks like, look no further than my article called Yet Another Way to Learn Recursion. However, to summarize, the process goes like this:
- Make a recursive call
- Pass a “smaller” version of the data into the recursive call
- Handle edge cases
- Profit
If you follow this process, I promise that you’ll stumble into fully working code most of the time. That said, I understand that the hardest part of this process is knowing what “smaller” means. Don’t worry! The next tip will cover that.
Consider the Classes of Recursive Problems
At first, recursion is going to seem really daunting, but there are always tricks to getting the right answer. For instance, you can actually group recursive problems into classes, which should give you less to think about when problem solving.
Now, I can’t say for certain what all of the classes of recursive problems are, but here are two major classes of problems:
- Recursion on sequences
- Recursion on trees
When I refer to recursion on sequences, what I’m really talking about is data that can be represented as a list (e.g., strings, arrays, and even numbers). If there is a way to think about the data in terms of “substrings” and “indices,” there’s a good chance the recursive solution falls in this category.
Alternatively, the data you’re working with is organized as a tree, a data structure that is inherently recursive (i.e., a tree contains subtrees). An example of a tree-like data structure is your file system (i.e., folders inside folders).
In my experience, problems that are tree-like tend to be easier to solve with recursion because your recursive calls are always made on subtrees. On the other hand, recursion on sequences is a bit harder because you have to think about how to break the sequence down into smaller parts—which is usually by removing an element and adding it back later.
That said, if you can figure out which class of recursive problem you’re dealing with, then you already have a strategy for solving it.
Build Confidence; Don’t Trace
Now, a tendency that folks have when first learning recursion is they want to figure out how a solution works at the most fundamental level. In general, I try to tell folks to avoid this temptation. However, if they really feel the need to dig deep, I usually ask them to follow a confidence building process.
Confidence building is a process somewhat similar to mathematical induction, though it reminds me more of substitution. The general idea is to take an existing recursive solution and test it on the smallest problem. In general, the “smallest problem” is going to fall right in line with the classes of problems mentioned above. In other words, the smallest sequence is usually going to be an empty sequence or a sequence containing a single value. Meanwhile, the smallest tree is usually going to be a single node.
If you can identify the smallest problem, you can create a test case to verify that the recursive function works. Then, you can craft a “next smallest problem” and test the function again. When you reach the part of the code that requires recursion, plug in the answer to the previous problem. If you’re strategic about how you do this, you’ll become confident that the method works.
What you absolutely should not do is trace the recursion. There are two main reasons for this:
- Your brain cannot physically track more than say five variables at a time; let alone multiple instances of those variables at different scopes.
- Tracing is prone to human errors that can propagate and take a lot of time to uncover.
So, while there is a temptation to trace the recursion because you want to prove to yourself that everything works, you’re going to find that it fries your brain very quickly. Recursion does not have to be this hard.
Draw a Picture
One tip that I think is nearly universal in the sciences is the value of drawing pictures. In general, the more confusing or complex the problem, the more I’m going to recommend drawing a picture. In fact, drawing is a wonderful tool for understanding recursion because the picture always ends up being a tree. Let me explain!
As a problem solving technique, recursion is quite different from iteration. Rather than repeating some action over and over again to solve a problem, we break our problem down into smaller and smaller problems until we find one we can solve. Here’s an example:
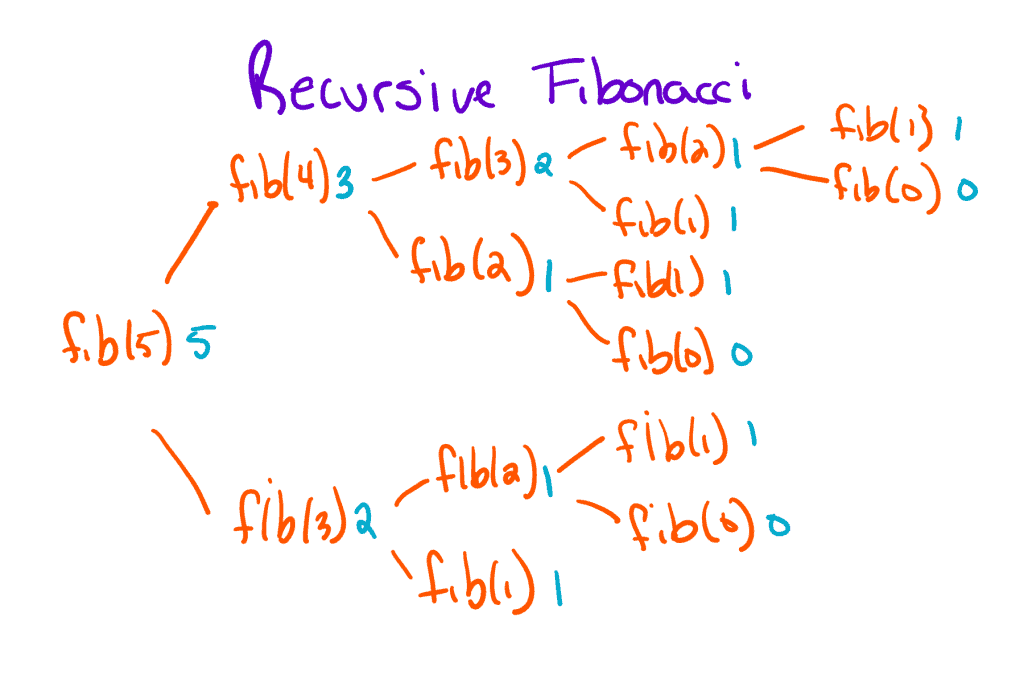
In this example, we’re trying to figure out the fifth term in the Fibonacci sequence. As it turns out, the fifth term can be written as the sum of the the fourth and third terms, so we draw those as children in our tree. Meanwhile, the fourth term can be broken down into the sum of the third and second terms. Eventually, if we keep breaking each problem down, we’ll hit a problem we can solve. In this case, there are actually two smallest problems: the first term and the zeroth term. With the answers to the smallest problems, we work backwards—summing the terms and using the answer to solve the next smallest problem.
Hopefully the part where we start working backwards makes sense. It’s the confidence building process that I mentioned above. As it turns out, it’s a core component of how recursion works.
Pivot to a Language Where Recursion Is the Norm
If recursion still stumps you after following these steps, it might be because recursion is sort of clunky in most languages. In general, the most popular languages all follow an imperative design (i.e., Java, C, Python, C#, etc.). In an imperative programming language, the bulk of our thinking goes into writing sequences of statements, which are somewhat antithetical to the concept of recursion. Or put another way, recursion and state don’t mix well.
Alternatively, recursion works really well in languages which are stateless (or as stateless as possible). These languages are called functional programming (fp) languages, and they work by treating all code as one giant expression to be evaluated. Because of this, the idea of a “smallest problem” is innate to the expression. After all, expressions are made of expressions.
Now, I should warn you. Functional languages are violently different from imperative languages. Here’s just an example of the Fibonacci problem solved in Lisp:
(defun fibonacci (n &optional (a 1) (b 1) (acc))
(if (<= n 0)
(reverse acc)
(fibonacci (- n 1) b (+ a b) (cons a acc))))
(defun countfibs(acc n fibs)
(if (< (length fibs) 1)
(reverse acc)
(countfibs (cons (list n (car fibs)) acc) (+ 1 n) (cdr fibs))))
(defun maybe-pos-int (input)
(cond
((null input) nil)
((string= input "") nil)
((every #'digit-char-p input) (parse-integer input))
(t nil)))
(defparameter num (maybe-pos-int (cadr *posix-argv*)))
(cond
((null num) (write-line "Usage: please input the count of fibonacci numbers to output"))
(t (dolist (item (countfibs (list) 1 (fibonacci num)))
(format t "~D: ~D~%" (car item) (cadr item)))))
For context, this was ripped from the Sample Programs repo
, which I maintain. The program does a little more than just dump the nth term (here’s the full description), but you get the idea. The first three blocks are function definitions and the last block is the expression evaluating the answer. Notice how the fibonacci and countfibs functions are recursive, and there are no variables floating around. If you’re curious about how lisp works, I wrote a mostly working interpreter in Java.
Anyway, I bring this up because there are languages out there that rely on recursion as their core mechanic. If you’re used to languages that have loops, you may find that learning recursion is difficult. Not to worry, recursion is just a different way of thinking, which you may pick up easier by working with a functional programming language like Lisp, Scheme, or Haskell.
With that said, that’s all I wanted to cover today. Ultimately, I wasn’t expecting to burn up 1500 words on this subject, but here we are. If you want to learn more about nerdy programming language stuff, check out one of these related resources:
- Which Programming Languages Index by One?
- The 28 Best Programming Languages of All Time
- There Is No Value in Ranking Programming Languages: The Cost of Gatekeeping in Tech
Yeah, that’s quite the series of posts, I know. I never claimed not to be a hypocrite. Anyway, take care! See you next time.
Recent Posts
While creating some of the other early articles in this series, I had a realization: something even more fundamental than loops and if statements is the condition. As a result, I figured we could...
Today, we're expanding our concept map with the concept of loops in Python! Unless you're a complete beginner, you probably know a thing or two about loops, but maybe I can teach you something new.